Polynomials & Factorisation

Question 1.
Find the degree of each of the polynomials given below,

i) x⁵- x⁴+ 3
Solution:
Degree is 5.

ii) x²+ x - 5
Solution:
Degree is 2.

iii) 5
Solution:
Degree is 0.

iv) 3x⁶+ 6y³ - 7
Solution:
Degree is 6.

v) 4 - y²
Solution:
Degree is 2.

vi) 5t - √3
Solution:
Degree is 1.

Question 2.
Which of the following expressions are polynomials in one variable and which are not ? Give reasons for your answer.

i) 3x² - 2x + 5
Solution:
Given expression is a polynomial in one variable.

ii) x²+ √2
Solution:
Given expression is a polynomial in one variable.

iii) p²- 3p + q
Solution:
Given expression is not a polynomial in one variable. It involves two variables p and q.

iv) y + 2/y
Solution:
Given expression is not a polynomial. Since the second term contains the variable in its denominator.

v)5√x + x√5
Solution:
Given expression is not a polynomial. Since the first term’s exponent is not an integer.

vi) x¹⁰⁰ + y¹⁰⁰
Solution:
Given expression has two variables. So it is not a polynomial in one variable.

Question 3.
Write the coefficient of x³in each of the following.

i) x³ + x + 1
ii) 2 - x³+ x²

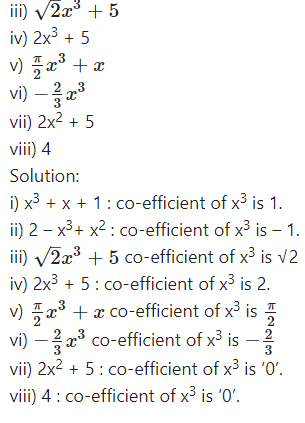
Question 4.
Classify the following as linear, quadratic and cubic polynomials.

• i) 5x²+ x - 7 : degree 2 hence quadratic polynomial.
• ii) x - x³, : degree 3 hence cubic polynomial.
• iii) x²+ x + 4 : degree 2 hence quadratic polynomial.
• iv) x - 1 : degree 1 hence linear polynomial.
• v) 3p : degree 1 hence linear polynomial.
• vi) πr²: degree 2 hence quadratic polynomial.

Question 5.
Write whether the following statements are True or False. Justify your answer.

• i) A binomial can have at the most two terms
• ii) Every polynomial is a binomial
• iii) A binomial may have degree 3
• iv) Degree of zero polynomial is zero
• v) The degree of x²+ 2xy + y²is 2
• vi) πr² is monomial

Solution :

• i) A binomial can have at the most two terms -True
• ii) Every polynomial is a binomial - False
• [∵ A polynomial can have more than two terms]
• iii) A binomial may have degree 3 - True
• iv) Degree of zero polynomial is zero - False
• v) The degree of x²+ 2xy + y² is 2 - True
• vi) πr²is monomial - True

Question 6.
Give one example each of a monomial and trinomial of degree 10.

Solution :
- 7x¹⁰ is a monomial of degree 10.
3x²y⁸ + 7xy - 8 is a trinomial of degree 10.

Question 1.
Find the value of the polynomial 4x²- 5x + 3, when

(i) x = 0
Solution:
The value at x = 0 is
4(0)²- 5(0) + 3
= 3

(ii) x = -1
Solution:
The value at x = -1 is
4 (- 1)² - 5 (- 1) + 3
= 4 + 5 + 3
= 12

iii) x = 2
Solution:
The value at x = 2 is
4(2)²- 5(2) + 3
= 16 -10 + 3
= 9

iv) x = 1/2
Solution:

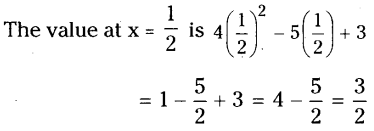
Question 2.
Find p(0), p(1) and p(2) for each of the following polynomials.

i) p(x) = x²- x + 1

Solution:
p(0) = 0²- 0 + 1 = 1
p(1) = 1²- 1 + 1 = 1
p(2) = 2²- 2 + 1 = 3

ii) P(y) = 2 + y + 2y²- y³
Solution:
p(0) = 2 + 0 + 2(0)²- 0³= 2
p(1) = 2+ 1 + 2(1)²- 1³= 4
p(2) = 2 + 2 + 2(2)²-2³= 4 + 8- 8 = 4

iii) P(z) = z³
Solution:
p(0) = 0³= 0
p(1) = 1³= 1
p(2) = 2³= 8

iv) p(t) = (t – 1)(t + 1) = t² - 1
Solution:
p(0) = (0 - 1) (0 + 1) = - 1
p(1) = t²- 1 = 1² - 1 = 0
p(2) = 2²- 1 = 4 - 1 = 3

v) p(x) = x² - 3x + 2
Solution:
p(0) = 0²- 3(0) + 2 = 2
p(1) = 1²- 3(1) + 2 = 1 - 3 + 2 = 0
p(2) = 2²- 3(2) + 2 = 4- 6 + 2 = 0

Question 3.
Verify whether the values of x given in each case are the zeroes of the polynomial or not ?

i) p(x) = 2x + 1; x = -1/2
Solution:
The value of p(x) at x = -1/2 is
p(-1/2)=2(-1/2)+1
= -1 + 1 = 0
∴ x = -1/2 is a zero of p(x).

(ii) p(x) = 5x - π ; x = ?3/2
Solution:
The value of p(x) at x = ?3/2 is
p(?3/2)=5(?3/2)?π=?15/2?π≠0
∴ x = ?3/2 is not a zero of p(x).

iii) p(x) = x² - 1; x = ±1
Solution:
The value of p(x) at x = 1 and - 1 is
p(1) = 1² - 1 = 0
p(-1) = (-1)² -1 = 0
∴ x = ±1 is a zero of p(x).

iv) p(x) = (x - 1) (x + 2); x = - 1, - 2
Solution:
The value of p(x) at x = - 1 is
p(-1) = (-1 - 1) (-1 + 2)
=-2 x 1 =-2 ≠ 0
Hence x = - 1 is not a zero of p(x).
And the value of p(x) at x = - 2 is
p (- 2) = (- 2 - 1) (- 2 + 2) = - 3 x 0 = 0
Hence, x = - 2 is a zero of p(x).

v) p(y) = y^{2; y = o
Solution:
The value of p(y) at y = 0 is p(0) = 02 = 0
Hence y = 0 is a zero of p(y).}

vi) p(x) = ax + b ; x = ?b/a
Solution:
The value of p(x) at x = ?ba is
p(?b/a)=a(?b/a)+b
= -b + b = 0
∴ x = ?ba is a zero of p(x).
vii) f(x) = 3x² - 1; x = ?1/√3, 2/√3
Solution:

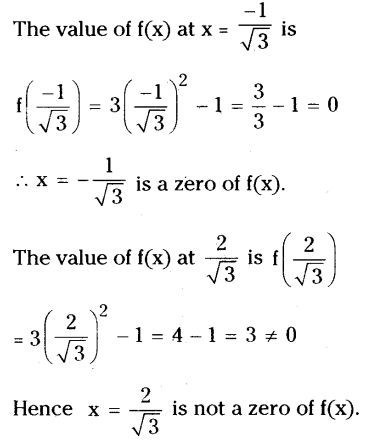
viii) f(x) = 2x - 1; x = 1/2; ?1/2
Solution:

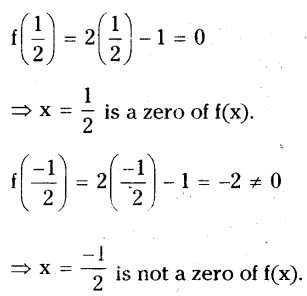
Question 4.
Find the zero of the polynomial in each of the following cases.

i) f(x) = x + 2
Solution:
x + 2 = 0
x = - 2
ii) f(x) = x - 2
Solution:
x - 2 = 0
x = 2
iii) f(x) = 2x + 3
Solution:
2x + 3 = 0
2x = - 3
x = ?3/2

iv) f(x) = 2x - 3 Solution: 2x - 3 = 0 2x = 3 x = 3/2 v) f(x) = x² Solution: x² = 0 x = 0 vi) f(x) = px, p ≠ 0 Solutin: px = 0 x = 0 vii) f(x) = px + q; p ≠ 0; p, q are real numbers. Solution: px + q = 0 px = -q x = ?q/p

Question 5.
If 2 is a zero of the polynomial p(x) = 2x²- 3x + 7a, find the value of

a

Solution:
Given that 2 is a zero of p(x) = 2x²- 3x + 7a
(i.e.) p(2) = 0
⇒ 2(2)²- 3(2) + 7a = 0
⇒ 8 - 6 + 7a = 0
⇒ 2 + 7a = 0
⇒ 7a = -2
⇒ a =-2/7

Question 6.
If 0 and 1 are the zeroes of the polynomial f(x) = 2x³ – 3x² + ax + b, find the values of a and b.

Solution:
Given that f(0) = 0; f(1) = 0 and
f(x) = 2x³- 3x²+ ax + b
∴ f(0) = 2(0)³- 3(0)²+ a(0) + b
⇒ 0 = b
Also f(1) = 0
⇒ 2(1)³- 3(1)²+ a(1) + 0 = 0
⇒ 2 - 3 + a = 0 .
⇒ a = 1
Hence a = 1; b = 0

Question 1.
Find the remainder when
x³+ 3x²+ 3x + 1 is divided by the following Linear polynomials i) x + 1 Each

Solution:
Let f(x) = x³+ 3x²+ 3x + 1
By remainder theorem, the remainder is f (- 1)
f (- 1) = (- 1)³+ 3(- 1)²+ 3(- 1) + 1
= - 1 + 3 - 3 + 1 = 0

ii) x ? 1/2
f(x) = x3 + 3x2 + 3x + 1
By remainder theorem, the remainder is f(1/2)

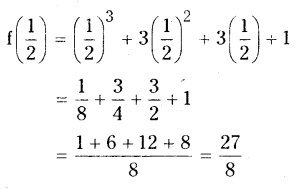
iii) x
Solution:
f(x) = x³+ 3x²+ 3x + 1
The remainder is f(0)
∴ f(0) = 0³+ 3(0)²+ 3(0) + 1 = 1

iv) x + π
Solution:
f(x) = x³+ 3x²+ 3x + 1
By remainder theorem, the remainder is f(- π)
f(- π) = (- π)³ + 3(-π)²+ 3 (-π) + 1 .
= π³+ 3π²- 3π + 1

v) 5 + 2x
f(x) = x³+ 3x²+ 3x + 1
The remainder is f(-5/2)

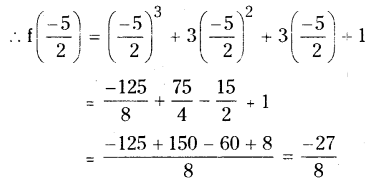
Question 2.
Find the remainder when x³- px²+ 6x - p is divided by x - p.

Solution:
Let f(x) = x³- px²+ 6x - p
(x - a) = x - p)
By Remainder theorem, the remainder is f(p)
∴ f(P) = P³- P(P)²+ 6p - p
= p³- p³+ 5p = 5p

Question 3.
Find the remainder when 2x²- 3x + 5 is divided by 2x - 3. Does it exactly divide the polynomial ? State reason.

Solution:
Let f(x) = 2x²- 3x + 5 and
x - a = 2x - 3 = x - 3/2
By Remainder theorem f(x) when divided by (x - 3/2) leaves a remainder f(3/2)

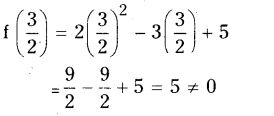
As the remainder is 5 we say that (2x - 3) is not a factor of f(x).

Question 4.
Find the remainder when 9x³- 3x²+ x - 5 is divided by x - 2/3

Solution:
Let f(x) = 9x³- 3x²+ x - 5
x-a = x - 2/3
Remainder theorem the remainder is f(2/3)

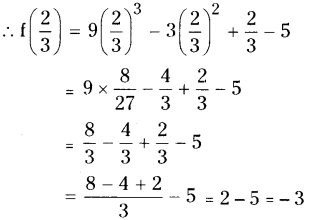
Question 5.
If the polynomials 2x³+ ax²+ 3x - 5 and x³+ x² – 4x + a leave the same remainder, when divided by x - 2, find the value of a.

Solution:
Let f(x) = 2x³+ ax²+ 3x - 5
g(x) = x³ + x²- 4x + a
Given that f(x) and g(x) divided x - 2
give same remainder.
i e., f(2) = g(2)
By Remainder theorem.
But f(2) = 2(2)³ + a(2)² + 3(2) - 5
= 2 x 8 + 4a + 6 - 5
= 17 +4a
g(2) = 2³+ 2²- 4(2) + a .
= 8 + 4 - 8 + a = 4 + a
i.e., 4 + a = 17 + 4a
∴ a - 4a = 17 - 4
– 3a = 13
a = -13/3

Question 6.
If the polynomials x³+ ax²+ 5 and x³- 2x²+ a are divided by (x + 2) leave the same remainder, find the value of a.

Solution:
Let f(x) = x³+ ax²+ 5
g(x) = x³- 2x²+ a
Given that when f(x) and g(x) divided by (x + 2) leaves the same remainder.
i.e.,f(-2) = g(-2)
By Remainder theorem
f(- 2) = (- 2)³+ a(- 2)²+ 5
= -8 + 4a + 5 = 4a - 3
g(- 2) = (- 2)³- 2(- 2)²+ a
= -8 - 8 + a = a - 16
By problem,
4a - 3 = a - 16
4a - a = - 16 + 3
⇒ 3a = - 13 ⇒ a = -13/3

Question 7.
Find the remainder when f(x) = x⁴- 3x²+ 4 is divided by g(x) = x - 2 and verify the result by actual division.

Solution:
Given f(x) = x⁴ - 3x²+ 4
g(x) = x - 2
The remainder when f(x) is divided by g(x) is f(2).
f(2) = 2⁴ - 3(2)² + 4
= 16 - 12 + 4
= 8
Actual division

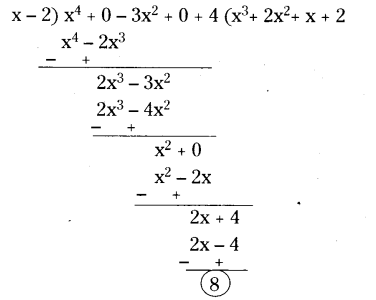
∴ The remainder either by Remainder theorem or by actual division is the same.

Question 8.
Find the remainder when p(x) = x³- 6x²+ 14x - 3 is divided by g(x) = 1 - 2x and verify the result by long division method.

Solution:
Given p(x) = x³ - 6x²+ 14x - 3
g(x) = 1 - 2x
By Remainder theorem when p(x) is divided by g(x) is p(1/2).

Question 9.
When a polynomial 2x³+ 3x²+ ax + b is divided by (x - 2) leaves remainder 2, and (x + 2) leaves remainder 2. Find a and b.

Solution:

Let f(x) = 2x³+ 3x²+ ax + b
The remainder when f(x) is divided by (x - 2) is 2.
i.e., f(2) = 2
⇒ 2(2)³+ 3(2)²+ a(2) + b = 2
⇒ 16 + 12 + 2a +b = 2
⇒ 2a + b = -26 …………………..(1)

Also the remainder when f(x) is divided by (x + 2) is – 2.
i.e., f(- 2) = - 2
⇒ 2(- 2)³+ 3(- 2)²+ a (- 2) + b = -2
⇒ -16 + 12 - 2a + b = -2
– 2a + b = 2 ………………..(2)
Solving (1) and (2),

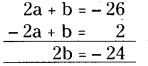
b = - 12
and 2a - 12 = - 26
2a = -26+ 12
a = -14/2 = -7,
a = -7, b = - 12

Question 1.
Determine which of the following polynomials has (x + 1) as a factor.

i) x³- x²- x + 1
Solution:
f(- 1) = (- 1)³- (- 1)²- (- 1) + 1
= -1 - 1 + 1 + 1 = 0
∴ (x + 1) is a factor.

ii) x⁴-x³+x²- x + 1
Solution:
f(- 1) = (- 1)⁴- (- 1)³+ (- 1)²- (- 1) + 1
= 1 + 1 + 1 + 1 + 1= 5
∴ (x + 1) is not a factor.

iii) x⁴+ 2x³+ 2x²+ x + 1
Solution:
f(- 1) = (-1)⁴+ 2 (- 1)³+ 2 (- 1)²+ (-1) + 1
= 1 - 2 + 2 - 1 + 1 = 1
∴ (x + 1) is not a factor.

iv) x³- x²- (3 - π3)x + π3
Solution:
f(- 1) = (- 1)³- (- 1)² - (3 - π3)(-1) + π3
= -1 -1 + 3 - π3 + π3 = 1
∴ (x + 1) is not a factor.

Question 2.
Use the factor theorem to determine whether g(x) is a factor of f(x) in each of the following cases:

i) f(x) = 5x³+ x²- 5x - 1; g(x) = x + 1
[Factor theorem : If f(x) is a polynomial; f(a) = 0 then (x - a) is a factor of f(x); a ∈ R]

Solution:
g(x) = x+ 1 = x- a say
∴ a = - 1
f(a) = f(- 1) = 5 (- 1)³+ (- 1)²- 5 (- 1) -1
= -5 + 1 + 5 - 1 = 0
∴ x + 1 is a factor of f(x).

ii) f(x) = x³+ 3x²+ 3x + 1; g(x) = x + 1
Solution:
g(x) = x + 1 = x - a
∴ a = - 1
f(a) = f(- 1) = (- 1)³+ 3 (- 1)²+ 3(-1) + 1
= -1 + 3 - 3 + 1 =0
∴ f(x) is a factor of g(x).

iii) f(x) = x³- 4x²+ x + 6;
g(x) = x - 2
Solution:
g(x) = x- 2 = x- a
∴ a = 2
f(a) = f(2) = 2³- 4(2)²+ 2 + 6
= 8 - 16 + 2 + 6 = 0
∴ g(x) is a factor of f(x).

iv) f(x) = 3x³+ x²- 20x +12; g(x) = 3x - 2
Solution:
g(x) = 3x - 2 = x- 2/3 = x - a
∴ a = 2/3

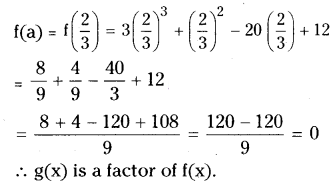
v) f(x) = 4x³+ 20x²+ 33x + 18; g(x) = 2x + 3
Solution:
g(x) = 2x + 3 = x + 3/2 = = x - a
∴ a = -3/2

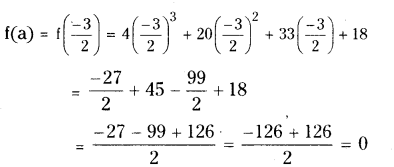
∴ g(x) is a factor of f(x).

Question 3.
Show that (x - 2), (x + 3) and (x - 4) are factors of x³- 3x²- 10x + 24.

Solution:
Given f(x) = x³- 3x²- 10x + 24
To check whether (x - 2), (x + 3) and (x - 4) are factors of f(x), let f(2), f(- 3) and f(4)
f(2) = 2³- 3(2)²- 10(2) + 24
= 8- 12-20 + 24 = 0
∴ (x - 2) is a factor of f(x).

f(- 3) = (- 3)³- 3(- 3)²- 10(- 3) + 24
= - 27 - 27 + 30 + 24 = 0
∴ (x + 3) is a factor of f(x).

f(4) = (4)³- 3 (4)²- 10 (4) + 24
= 64 - 48 - 40 + 24
= 88 - 88
= 0
∴ (x - 4) is a factor of f(x).

Question 4.
Show that (x + 4), (x – 3) and (x – 7) are factors of x³ – 6x² – 19x + 84.

Solution:
Let f(x) = x³- 6x²- 19x + 84
To verify whether (x + 4), (x - 3) and (x - 7) are factors of f(x) we use factor theorem.

Let f(- 4), f(3) and f(7)
f(- 4) = (- 4)³- 6 (- 4)²- 19 (- 4) + 84
= -64 - 96 + 76 + 84
= 0 .
∴ (x + 4) is a factor of f(x).

f(3) = 3³- 6(3)²- 19(3) + 84
= 27 - 54 - 57 + 84
= 0
∴ (x - 3) is a factor of f(x).

f(7) = 7³- 6(7)²- 19(7) + 84
= 343 - 294 - 133 + 84
= 427 - 427
= 0
∴ (x - 7) is a factor of f(x).

Question 5.
If both (x - 2) and (x - 1/2)of px²+ 5x + r, show that p = r.

Solution:
Let f(x) = px²+ 5x + r
As (x - 2) and (x - 1/2)are factor of f(x), we have f(2) = 0 and f(1/2) = 0
∴ f(2) = p(2)²+ 5(2) + r
= 4p + 10 + r = 0
= 4p + r
= -10 ………………(1)

⇒ p + 10 + 4r = 0
⇒ p + 4r = - 10 ………………. (2)
From (1) and (2);
4p + r = p + 4r
4p - p = 4r - r
3p = 3r
∴ P = r

Question 6.
If (x²- 1) is a factor of ax⁴+ bx³+ cx²+ dx + e, show that a + c + e = b + d = 0.

Solution:
Let f(x) = ax⁴+ bx³+ cx²+ dx + e
As (x - 1) is a factor of f(x) we have
x²- 1 = (x + 1) (x - 1) hence f(1) = 0 and f(-1) = 0
f(1) = a + b + c + d + e = 0 ……………. (1)
and f(-1) = a- b + c- d + e = 0
⇒ a + c + e = b + d
Substitute this value in equation (1)
a + c + e + b + d=0
b + d + b + d=0
2 (b + d) = 0
⇒ b + d = 0
∴ a + c + e = b + d = 0

Question 7.
Factorise

i) x³- 2x²- x + 2

Solution:
Let f(x) = x³- 2x²- x + 2
By trial, we find f(l) = 1³- 2(1)²- 1 + 2
= 1 - 2 - 1 + 2
= 0 .
∴ (x - 1) is a factor of f(x).
[by factor theorem]
Now dividing f(x) by (x - 1).

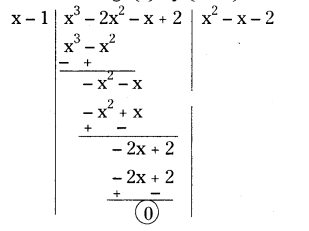
f(x) = (x - 1) (x²- x - 2)
= (x - 1) [x²- 2x + x- 2]
= (x - 1) [x (x - 2) + 1 (x - 2)]
= (x - 1) (x - 2) (x + 1)

ii) x³- 3x²- 9x - 5
Solution:
Let f(x) = x³- 3x²- 9x - 5By trial,
f(- 1) = (- 1)³- 3(- 1)²- 9(- 1) - 5
=-1 - 3 + 9 - 5
=0
∴ (x + 1) is a factor of f(x).
[ ∵ by factor theorem]
Now dividing f(x) by (x + 1).

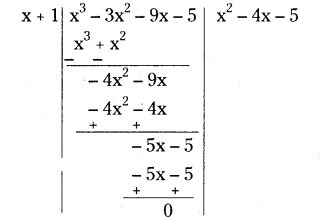
f(x)=(x + 1)(x²- 4x - 5)
But x²- 4x - 5 = x²- 5x + x - 5
= x (x - 5) + 1 (x - 5)
=(x - 5)(x + 1)
∴ f(x)=(x + 1)(x + 1)(x - 5)

iii) x³+ 13x²+ 32x + 20
Solution:
Let f(x) = x³+ 13x²+ 32x + 20
Let f(- 1)
= (- 1)³+ 13 (- 1)²+ 32 (- 1) + 20
= - 1 + 13 - 32 + 20 = 33 - 33 = 0
∴ (x + 1) is a factor of f(x).
[ ∵ by factor theorem] Now dividing f(x) by (x + 1).

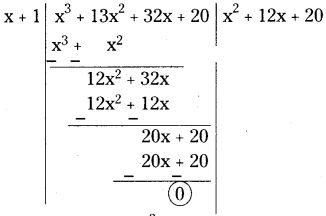
iv) y³+ y²- y - 1
Let f(y) = y³+ y²- y - 1
f(1) = 1³+ 1²- 1 - 1 = 0
(y - 1) is a factor of f(y).
Now dividing f(y) by (y - 1).

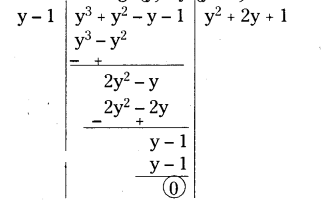
∴ f(x) = (x + 1)(x²+ 12x + 20)
But (x²+ 12x + 20) = x²+ 10x + 2x + 20
=x(x + 10)+2(x + 10)
=(x + 10)(x + 2)
∴f(x) = (x + 1)(x + 2)(x + 10)

Question 8.
If ax²+ bx + c and bx²+ ax + c have a common factor x + 1 then show that c = 0 and a = b.

Solution:
Let f(x) = ax²+ bx + c and g(x) = bx²+ ax + c given that (x + 1) is a common factor for both f(x) and g(x).
∴ f(-1) = g(- 1)
⇒a(- 1)²+ b(- 1) + c
= b(- 1)²+ a (- 1) + c
⇒ a - b + c = b - a + c
⇒ a + a = b + b
⇒ 2a = 2b
⇒ a = b
Also f(- 1) = a - b + c = 0
⇒ b - b + c = 0
⇒ c = 0

Question 9.
If x²- x - 6 and x²+ 3x - 18 have a common factor x - a then find the value of a.

Solution:
Let f(x) = x²- x - 6 and
g(x) = x²+ 3x - 18
Given that (x - a) is a factor of both f(x) and g(x).
f(a) = g(a) = 0
⇒ a²- a - 6 =a²+ 3a - 18
⇒ - 4a = - 18 + 6
⇒ - 4a = - 12
∴ a = 3

Question 10.
If (y - 3) is a factor of y³- 2y²- 9y + 18, then find the other two factors.

Solution:
Let f(y) = y³- 2y²- 9y + 18
Given that (y - 3) is a factor of f(y).
Dividing f(y) by (y - 3)

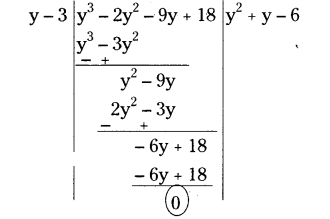
∴ f(y) = (y - 3) (y + y - 6)
But y²+ y - 6
= y²+ 3y - 2y - 6
= y (y + 3) - 2 (y + 3)
= (y + 3) (y - 2)
∴ f(y) = (y - 2)(y - 3)(y + 3)
The other two factors are (y - 2) and (y + 3).

Question 1.
Use suitable identities to find the following products.

i) (x + 5) (x + 2)

Solution:
(x + 5) (x + 2)
= x²+ (5 + 2)x + 5 x 2
[ ∵ (x + a) (x + b) = x²+ (a + b) x + ab]
= x²+ 7x + 10

ii) (x - 5) (x - 5)
Solution:
(x - 5) (x - 5)
= (x - 5)²= x²- 2(x) (5) + 5²
[ ∵(x - y)²= x²- 2xy + y²]
= x²- 10x + 25

iii) (3x + 2) (3x - 2)
Solution:
(3x + 2) (3x - 2) = (3x)²- (2)²
[∵ (x + y) (x - y) =x²- y²]
= 9x²- 4

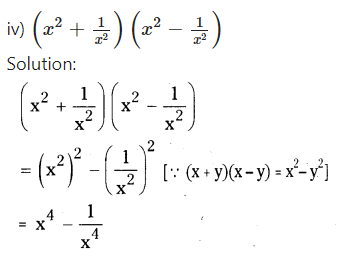
v) (1 + x) (1 + x)
Solution:
(1 + x) (1 + x)
= (1 + x)²= 1²+ 2 (1) (x) + x²
[∵(x + y)²= x²+ 2xy + y²]
= 1 + 2x + x²

Question 2.
Evaluate the following products with¬out actual multiplication.
i) 101 x 99
Solution:
101 x 99
= (100 + 1) (100 - 1)
= 100²- 1²
= 10000 - 1
= 9999

ii) 999 x 999
Solution:
999 x 999
= 999²
= (1000 - 1)²
= 1000²- 2 x (1000) x 1 + 1²
= 1000000-2000 + 1
= 998001

iii) 50 1/2 × 49 1/2 Solution:

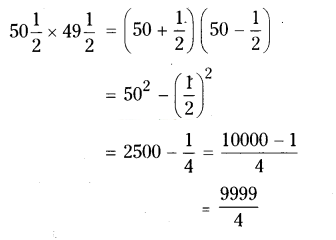
iv) 501 x 501
Solution:
501 x 501
= (500 + 1) (500 + 1)
= (500 + 1)²
= 500²+ 2 x (500) x 1 + 1²
= 250000 + 1000 + 1 = 251001

v) 30.5 x 29.5 = (30 + 0.5) (30 - 0.5)
= 30²- (0.5)²
= 900 - 0.25
= 899.75

Question 3.
Factorise the following using appro-priate identities.

i) 16x²+ 24xy + 9y²

Solution:
16x²+ 24xy + 9y2
= (4x)²+ 2 (4x) (3y) + (3y)²
= (4x + 3y)²= (4x + 3y) (4x + 3y)
[ ∵ (x + y)²= x²+ 2xy + y²]

ii) 4y²- 4y + 1
Solution:
4y²- 4y + 1
= (2y)²- 2 (2y) (1) + (1)²
[ ∵ (x -y)²= x²- 2xy + y²]
= (2y -1)²= (2y - 1) (2y-1)

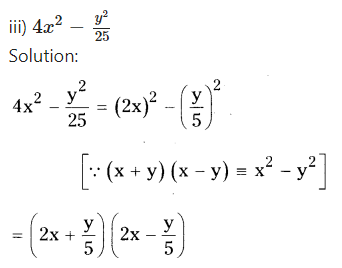
iv) 18a²- 50
Solution:
18a²- 50 = 2 (9a²- 25)
= 2[(3a)²- (5)²]
[ ∵ x²- y²= (x + y) (x - y)]
= 2 (3a + 5) (3a - 5)

v) x²+ 5x + 6
Solution:
x²+ 5x + 6 = x²+ (3 + 2) x + 3 x 2
[ ∵ (x + a) (x + b) = x²+ (a + b) x + a . b]
= (x + 3) (x + 2)

vi) 3p²- 24p + 36
Solution:
3p²- 24p + 36
= 3[p²- 8p + 12]
= 3[p²+ (- 6 - 2)p + (- 6) (- 2)]
[ ∵ (x + a) (x + b) = x²+ (a + b) x + ab]
= 3 (p - 6) (p - 2)

Question 4.
Expand each of the following, using suitable identities.

i) (x + 2y + 4z)2
(x + 2y + 4z)²= (x)²+ (2y)²+ (4z)²+ 2(x) (2y) + 2 (2y) (4z) + 2 (4z) (x)
[ ∵ (x + y + z)²= x²+ y²+ z²+ 2xy + 2yz + 2zx]
= x²+ 4y²+ 16z²+ 4xy + 16yz + 8zx

ii) (2a - 3b)³
Solution:
(2a - 3b)³= (2a)³- 3 (2a)²(3b) + 3 (2a) (3b)²- (3b)³
[ ∵ (a - b)³= a³- 3a²b + 3ab²- b³]
= 8a³- 3(4a²) (3b) + 3 (2a) (9b²) - 27b³
= 8a³- 36a²b + 54ab²-27b³
(or)
∵ (a - b)³= a³- b³- 3ab (a - b)]
= (2a)³- (3b)³- 3(2a) (3b) (2a - 3b)
= 8a³- 27b³- 18ab (2a - 3b)

iii) (- 2a + 5b - 3c)²
Solution:
(- 2a + 5b - 3c)²
= (- 2a)²+ (5b)²+ (- 3c)²+ 2 (- 2a) (5b) + 2 (5b) (- 3c) + 2 (- 3c) (- 2a)
= 4a²+ 25b²+ 9c²- 20ab - 30bc + 12ca
[ ∵ (x + y + z)²= x²+ y²+ z²+ 2xy +2yz +2za]

iv) [a/4 ? b/2 + 1]²
Solution:

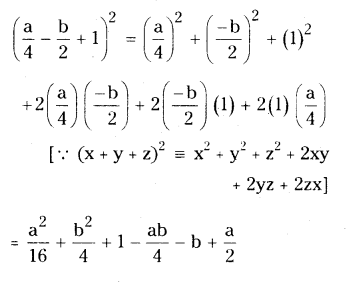
v) (p + 1)³
Solution:
(p + 1)³
= (P)³+ 3 (p)²(1) + 3 (p) (1)²+ (1)³
[ ∵ (x + y)³= x³+ 3x²y + 3xy²+ y³]
= p³+ 3p²+ 3p + 1

vi) (x ? 2/3 y)³
Solution:

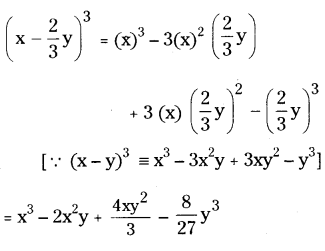
Question 5.
Factorise

i) 25x²+ 16y²+ 4z²- 40xy + 16yz - 20xz
Solution:
25x²+ 16y²+ 4z²- 40xy + 16yz - 20xz
= (5x)²+ (- 4y)²+ (- 2z)²+ 2(5x) (- 4y) + 2 (- 4y) (- 2z) + 2 (- 2z) (5x)
= (5x - 4y - 2z)²= (- 5x + 4y +, 2z)²

ii) 9a²+ 4b²+ 16c²+ 12ab - 16bc - 24ca
Solution:
9a²+ 4b²+ 16c²+ 12ab - 16bc -24ca
= (3a)²+ (2b)²+ (- 4c)²+ 2 (3a) (2b) + 2 (2b) (- 4c) + 2(- 4c) (3a)
= (3a + 2b - 4c)²

Question 6.
If a + b + c = 9 and ab + be + ca = 26, find a²+ b²+ c².

Solution:
Given that a + b + c = 9
Squaring on both sides,
(a + b + c)²= 9²
⇒ a²+ b²+ c²+ 2 (ab + be + ca) = 81 ⇒ a²+ b²+ c²= 81 - 2 (ab + be + ca)
(by problem)
= 81 - 2 x 26
= 81 - 52 = 29

Question 7.
Evaluate the following by using suit¬able identities. m EachgM)

i) (99)³
Solution:
(99)²= (100 - 1)³
= 100³- 3 (100)²(1) + 3 (100) (1)²- 1³
[ ⇒ (x - y)³= x³- 3x²y + 3xy²+ y³]
= 1000000 - 30000 + 300 - 1
= 970299

ii) (102)³
Solution:
(102)³= (100 + 2)³
= 100³+ 3 (100)²(2) + 3 (100) (2)²+ 2³
[ ⇒ (x + y)³= x³+ 3x²y + 3xy²+ y³]
= 1000000 + 60000 + 1200 + 8
= 1061208

iii) (998)³
Solution:
(998)³=(1000 - 2)³
[ ⇒ (x - y)³= x³- 3x²y + 3xy²- y³] = 1000³- 3(1000)²(2) + 3(1000)(2)²- 2³
= 1000000000 - 6000000 + 12000 - 8
= 994011992

iv) (1001)³
Solution:
(1001)³= (1000 + 1)³.
[ ⇒ (x + y)³= x³+ 3x²y + 3xy²+ y³] = 1000³+ 3(1000)²(1) + 3(1000) (1)²+ 1³
= 1000000000 + 3000000 + 3000 + 1
= 1003003001

Question 8.
Factorise each of the following.

i) 8a³+ b³+ 12a²b + 6ab²
Solution:
8a³+ b³+ 12a²b + 6ab²
= (2a)³+ (b)³+ 3 (2a)²(b) + 3 (2a) (b)²
= (2a + b)³

ii) 8a³- b³- 12a²b + 6ab²
Solution:
8a³- b³- 12a²b + 6ab²
= (2a)³- (b)³- 3 (2a)²(b) + 3 (2a) (b)²
= (2a - b)³

iii) 1 - 64a³-12a + 48a²
Solution:
1 - 64a³- 12a + 48a²
= (1)³- (4a)³- 3(1)²(4a) + 3(1) (4a)²
= (1 - 4a)³

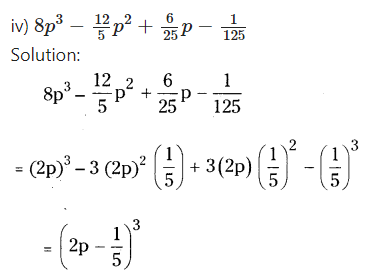
Question 9.
Verify i) x³+ y³= (x + y) (x²- xy + y²);

ii) x³- y³= (x - y) (x²+ xy + y²)
Using some non-zero positive integers and check by actual multiplication. Can you
call these as identities ?
i) x³+ y³= (x + y) (x²- xy + y²)
Solution:
Given x³+ y³= (x + y) (x²- xy + y²)
L.H.S = x³+ y³
R.H.S = (x + y) (x²- xy + y²)
= x (x²- xy + y²) + y (x²- xy + y²)
= x³-x²y + xy²+ x²y - xy²+ y³
= x³+ y³
= L.H.S
∴ L.H.S = R.H.S

Take x = 3, y = 2
L.H.S = 3³+ 2³= 27 + 8 = 35
R.H.S = (3 + 2) (3²- 3 x 2 + 2²)
= 5 x (9 - 6 + 4)
= 5 x 7 = 35
∴ L.H.S = R.H.S

ii) x³- y³= (x - y) (x²+ xy + y²)
Solution:
Given that x³- y³= (x - y) (x²+ xy + y²)
L.H.S = x³- y³
R.H.S = (x - y) (x²+ xy + y²)
= x (x²+ xy + y²) - y (x²+ xy + y²)
= x³+ x²y + xy²- x²y - xy²- y³
= x³- y³= L.H.S

L.H.S = 3³- 2³= 27 - 8 = 19
R.H.S = (3 - 2) (3²+ 3 x 2 + 2²)
= 1 x (9 + 6 + 4)
= 1 x 19 = 19
∴ L.H.S = R.H.S
We can call the above two expressions as identities

Question 10.
Factorise by using the above results (identities).

i) 27a³+ 64b³
Solution:
27a³+ 64b³= (3a)³+ (4b)³
= (3a + 4b) {(3a)²- (3a) (4b) + (4b)²}
= (3a + 4b) (9a²- 12ab + 16b²)

ii) 343y³- 1000
Solution:
343y³- 1000 = (7y)³- (10)³
= (7y - 10) [(7y)²+ (7y) (10) + (10)²]
= (7y - 10) (49y²+ 70y + 100)

Question 11.
Factorise 27x³+ y³+ z³- 9xyz using identity.

Solution:
Given 27x³+ y³+ z³- 9xyz
= (3x)³+ (y)³+ (z)³- 3 (3x) (y) (z)
= (3x + y + z)
[(3x)²+ y²+ z²- (3x) (y) - (y) (z) - (z) (3x)]
[ ⇒ (x³+ y³+ z³- 3xyz = (x + y + z) (x²+ y²+ z²- xy - yz - zx)
= (3x + y + z) (9x²+ y²+ z²- 3xy - yz - 3xz)

Question 12.
Verify that x³+ y³+ z³- 3xyz = 1/2 (x + y + z) [(x - y)²+ (y - z)²+ (z - x)²]
(OR)
Verify that
p³+ q³+ r³- 3pqr = 1/2 (p + q + r)
[(p - q)²+ (q - r)²+ (r - p)²]

Solution:
Given x³+ y³+ z³- 3xyz = 1/2 (x + y + z) [(x - y)²+ (y - z)²+ (z - x)²]
R-H.S = 1/2 (x + y + z) [(x - y)²+ (y - z)²+ (z - x)²]
= 1/2 (x + y + z) [x²+ y²- 2xy + y²+ z²- 2yz + z²+ x²- 2xz]
= 1/2 (x + y + z) [2x²+ 2y²+ 2z²- 2xy - 2yz - 2zx]
= 1/2 (x + y + z) (2) [x²+ y²+ z²- xy - yz - zx]
= (x + y + z) (x²+ y²+ z²- xy - yz - zx)
= L.H.S
Hence proved.

Question 13.
If x + y + z = 0, show that x³+ y³+ z³= 3xyz

Solution:
Given x + y + z = 0
To prove x³+ y³+ z³= 3xyz
We have an identity
(x + y + z) (x²+ y²+ z²- xy - yz - zx)
= x³+ y³+ z³- 3xyz
Substituting x + y + z = 0in the above equation, we get
0 x (x²+ y²+ z²-xy-yz-zx)
= x³+ y³+ z³- 3xyz
⇒ x³+ y³+ z³- 3xyz = 0
⇒ x³+ y³+ z³= 3xyz

Question 14.
Without actual calculating the cubes, find the value of each of the following.

i) (- 10)³+ 7³+ 3³

Solution:
Given (-10)³+ 7³+ 3³
Sum of the bases = -10 + 7 + 3 = = 0
∴ (- 10)³+ 7³+ 3³
= 3 (- 10) x (7) x 3
= -630
[ ∵ x + y + z = 0 then x³+ y³+ z³= 3xyz]

ii) (28)³+ (- 15)³+ (- 13)³
Solution:
Given (28)³+ (- 15)³+ (- 13)³
Sum of the bases = 28 + (- 15) + (- 13) = 0
∴ (28)³+ (- 15)³+ (- 13)³
= 3 x 28 x (- 15) x (- 13)
= 16380

iv) (0.2)³- (0.3)³+ (0.1)³
Solution:
Given that (0.2)³- (0.3)³+ (0.1)³
= (0.2)³+ (- 0.3)³+ (0.1)³
Sum of the bases = 0.2 - 0.3 + 0.1 = 0
∴ (0.2)³+ (-0.3)³+ (0.1)³
= 3 x (0.2) (- 0.3) (0.1)
= -0.018

Question 15.
Give possible expressions for the length and breadth of the rectangle whose area is given by

i) 4a²+ 4a - 3
Given that area = 4a²+ 4a - 3
= 4a²+ 6a - 2a - 3
= 2a (2a + 3) - 1 (2a + 3)
= (2a - 1) (2a + 3)
∴ Length = (2a + 3); breadth = (2a - 1).

ii) 25a²- 35a + 12
Solution:
Given that area = 25a²- 35a +12
= 25a²- 20a - 15a + 12
= 5a (5a - 4) - 3 (5a - 4)
= (5a – 4) (5a - 3)
∴ (5a - 4) (5a - 3) are the length and breadth.

Question 16.
What are the possible polynomial expressions for the dimensions of the cuboids whose volumes are given below ?

i) 3x³- 12x

Solution:
Volume = 3x³- 12x
= 3x (x²- 4)
= 3x (x + 2) (x - 2) are the dimensions.

ii) 12y²+ 8y - 20
Solution:
Given that volume = 12y²+ 8y - 20
= 4 (3y²+ 2y - 5)
= 4 [3y²+ 5y - 3y - 5]
= 4 [y (3y + 5) - 1 (3y + 5)]
= 4 (3y + 5) (y - 1)
Hence 4, (3y + 5) and (y - 1) are the dimensions.

Question 17.
Show that if 2 (a²+ b²) = (a + b)²then a = b

Solution:
Given that 2 (a²+ b²) = (a + b)²
To prove a = b
As 2 (a²+ b²) = (a + b)²
We have
2a²+ 2b²= a²+ 2ab + b²
2a²- a²+ 2b²- b²= 2ab
a²+ b²= 2ab
This is possible only when a = b
∴ a = b